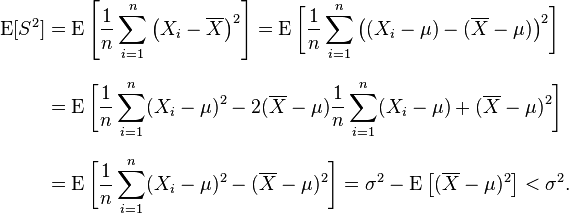Hola MediaVideros! Tengo parcial este Lunes y esta asignatura me lleva de cabeza, no me aclaro y en internet no encuentro muchos recursos.
Mis dudas son especialmente sobre las propiedades de los estimadores (Insesgadez, consistencia y eficiencia).
Respecto a la insesgadez sé como saber si un estimador es insesgado o no, pero no se cuando es asintóticamente insesgado (Creo que es para muestras grandes, es decir, el límite cuando n tiende a infinito, del sesgo, que tiene que dar 0; pero no sé aplicarlo). Por ejemplo en el caso de que, trabajando con muestras aleatorias simples, sepa que la cuasivarianza muestral es un estimador insesgado de la varianza poblacional, la varianza muestral sólo lo es asintóticamente.
Con la consistencia sí que no me entero. No sé como demostrar que la cuasivarianza y la varianza muestral son consistentes cuando la distribución poblacional es la normal, por ejemplo.
En el caso de la eficiencia, calculando la cota de Freddet Crammer Rao y, sabiendo que la varianza del estimador alcanza dicha cota, dicho estimador es eficiente?
Gracias!