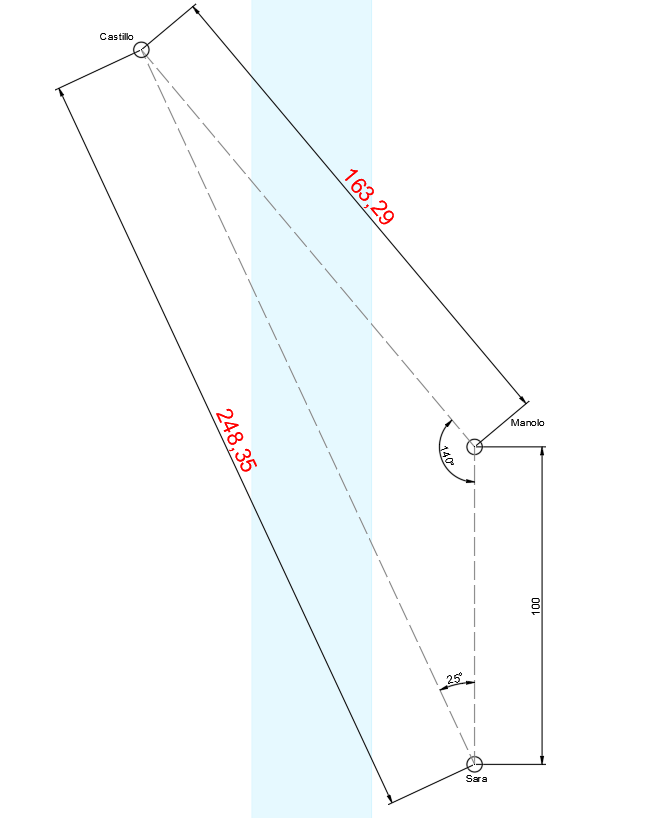
Sara y Manolo quieren saber a qué distancia se encuentra un castillo que está en la
orilla opuesta de un río. Se colocan a 100 metros de distancia el uno del otro y consideran el
triángulo en cuyos vértices están cada uno de los dos, y el castillo. El ángulo correspondiente al
vértice en el que está Sara es de 25° y el ángulo del vértice en el que está Manolo es de 140°. ¿A qué
distancia se encuentra Sara del castillo? ¿Y Manolo?
Hay q hallar los lados x e y con el teorema del coseno?? Esq hallando el lado x me salen 2483,5 m y no me cuadra. No encuentro este problema concretamente por ninguna parte. Si alguien pudiera explicarme el problema lo agradecería porque en trigonometria voy bastante perdido