
Te lo pongo en pseudocódigo, yo creo que es algo así:
if reduce( x,y=> x+y, flat(array)) > 10000 ? print "que números más grandes tienes!!!!" : print "hahaha el señor de los numéritos pequeños!!!"
#30539 Si buscas la metodología para afrontar estos problemas, yo buscaría el patrón, en este caso se suma en la primera fila 1,2,3,4, la segunda fila suma 2,3,4,4. Hay un patrón en la suma y va rotando en cada fila, el número máximo es n-1, con esto ya puedes sacar el resultado.
No es la forma más elegante de hacerlo tampoco
en este caso se suma en la primera fila 1,2,3,4, la segunda fila suma 2,3,4,4. Hay un patrón en la suma y va rotando en cada fila, el número máximo es n-1
wat? ese no es el patrón... es que los números están en diagonal de arriba a abajo y de derecha a izquierda

#30545 Y va diciendo por ahí que la informática no es una ingeniería. Putos telecos lo tontacos que son jajajaja.
#30519 Yo siempre los saco a base de prueba y error, pero vamos nunca se me dieron bien este tipo de ejercicios. Es más, lo leí y dije "bu pero es facil", hice un bucle guarrero y me quedé tan feliz, luego me di cuenta de que solo sacaba media matriz xD
Estaba con otras cosas y me quedó la espinita asi que lo saqué de todo (en 2 bucles, no se si se puede hacer en 1). Te puedo decir que te fijes en como crecen y decrecen los índices (vamos que sigas la idea que desglosas) y ahí veras un patrón.
La primera coordenada hace algo como 0 : 0 - 1 : 0 - 1 - 2 : 0 - 1 - 2 - 3, etc
La segunda coordenada hacer algo como 0 : 1 - 0: 2 - 1 - 0: 3 - 2 - 1 - 0, etc
Ahí tienes el primer bucle (te diría que sacases el bucle que te permite calcular una de las coordenadas y luego reutilizarlo para calcular la otra operando)
El segundo bucle es lo mismo pero el patrón es un poco más raro.
no se si me estoy explicando una mierda xDDD
Si el código (chustero) en python te vale de algo te lo paso xD
Sigo sin entender lo que dices, si n es siempre impar, hay (n*2)-1 diagonales, la longitud de la diagonal es x+1 hasta llegar a i==n, que pasa a ser x-1 , siendo n la dimensión del array, i la iteración actual, x el acumulador de cada iteración
#30549 No te pongas tan nervioso, entiendo que quieres mantener el personaje que te has montado pero no es necesario alterarse tanto.
Mi patrón de arriba es correcto y la matriz debería de salir, la solución del tirón no la conozco.
#30551 Esta solución es para todo n >1, lo digo por si alguien mete un 1 ahí o vete a saber.
A partir de 1, sumas lo que puse arriba, 1,2,3,4...(n-1), al valor anterior, es decir -> 1,2,4,7,11.
Al bajar a la siguiente fila, corres este patrón hacia la izquierda, en ese caso es 2,3,4,4 -> 3,5,8,12,16
El número máximo al que llegas es n-1, llegado a la mitad de la matriz, empiezas a descender en el sumatorio, 1234444321
edit: me lo vuelvo a mirar, a ver.
#30550 Si, se como dices, estos ejercicios son una rayada mental impresionante xD Me siento muy estúpido porque el patrón que sigue lo tengo claro y no hay huevos a codificar eso luego, bueno, mas que codificar a sacar el algoritmo, codificar es lo de menos.
#30556 menudo navajazo le metia
Luego tengo el siguiente cuando acabe para entretenerme haciendo espirales
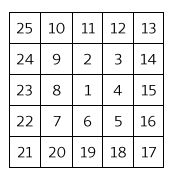
Menos mal que son los "sencillos"
vengo de dar una charla sobre rust y al terminar uno me pregunta que si rust tiene mocks xddd
putos javeros, son adorables
La clave hacerlo para un 2x2, lo haces para un 3x3 y si no ves un patrón al 4x4 frena jajaja
Lo haría pero el Apex me espera
#30557 Este en concreto me lo sé, o es muy parecido, lo hice project euler:

#30556 Pues no me lo he mirado que ando de culo con el trabajo. Pero con la tontería si... este tipo de ejercicio es lo que suelo programar en el curro, hago bastante algoritmica xd
#30534 Con T class te refieres a un génerico? xddd
Pregunta que te lo respondo en serio si lo sé.
Yo lo he "resuelto" así, sabiendo que me dan el tamaño, representando los movimientos ( algo como un dag )

#30565 Bueno... yo no lo hago en bucles, lo explicaré para el tonto de telecos, entiendo que no tenga mucha idea de mates... Lo estoy resolviendo como aplicando vectores a los indices...
incializo 00 paso a 01 ,
vector -1-1 +1+1
vector 2(-1-1) 2(+1+1)
vector 3(-1-1) 3(+1+1)
vector k(-1-1) k(+1+1)
...
Hasta la condicion y pasas a disminuir k.
Y un paso final.
Diría que lo he dicho bien, quizás me equivoco, quizás es lo que ha dicho el de arriba, yo entiendo que él lo hace con 3 bucles, le he dedicado 5 minutos.. xd sorry si la lio
#30562 Falta de alineación (pese a la hoja de cuadros) y uso de 4 patrones distintos de "1"s son claros indicativos de que no programas nunca en papel y de que eres un psicópata.